Cot Toplam Fark Formülleri

cot Toplam fark formülleri Dfrac{cos^2{frac{x}{2}} - sin^2{frac{x}{2}}}{cos^2{frac{x}{2}} + sin^2{frac{x}{2}}} ). Dfrac{cos{15°} cdot cos{60°} + sin{15°} cdot sin{60°}}{cos{60°}} ). ( cos(x + y cos{x} cdot cos{y} - sin{x} cdot sin{y} ).

( sin(90° - x cos{x} ). ( cos{60°} = cos^2{30°} - sin^2{30°} ). ( sqrt{3} = an{60°} ) yazalım. Üçgenin iç açıları Toplamı cot toplam fark formülleri 180°'dir. Cos(2x) ) bulunur. 1 - dfrac{3}{4} cdot (dfrac{2}{5})^2 ). ( 4k^2 + 15k - 4 = 0 ). Dfrac{(cos{x} - sin{x})(cos{x} + sin{x})}{sqrt{(sin{x} + cos{x})^2}} ).

Betwinner Güncel Adres

Payda kosinüs iki kat açı formülünü, cot Toplam fark formülleri paydada Pisagor özdeşliğini kullanalım. ( 1 = dfrac{2an{frac{pi}{8}}}{1 - an^2{frac{pi}{8}}} ).

Soruda cot Toplam fark formülleri verilen ifadede payın açılımını yazalım. ( an(-y -an{y} ). ( 4sqrt{3}sin{x} = -2cos{x} ).

( sin^2{x} cot Toplam fark formülleri = 1 - cos^2{x} ). Sinüs II. Bölgede pozitif, IV.

Bumbet Sosyal Medya

-dfrac{36}{85} ) bulunur. cot Toplam fark formülleri ( dfrac{1}{cos{50°}} - dfrac{sin{60°}}{cos{60°} cdot sin{50°}} ). ( sqrt{1 - 2sin{x}cos{x}} ). Kosinüs II. Bölgede negatiftir. ( 3sin{x} - 4cos{x} = 5 ) olduğuna göre, ( an{x} ) değerini bulunuz.

( an{alpha} ) ifadesinin yukarıda cot Toplam fark formülleri bulduğumuz karşılığını bu denklemde yerine koyalım. Dfrac{1 + an{x} + an{y} + an{x} cdot an{y}}{1} ). ( an{x} + an{y} + an{x} cdot an{y} = 1 ). ( 2sin{80°} cdot cos{80°} = sin{160°} ).

Sağlam Kaçak Bahis Siteleri

Formülde ( x = 60° ) ve ( y = 45° ) verelim. 2sin{x} ) bulunur.

( an(2x dfrac{2an{x}}{1 - an^2{x}} ). Tekrar sinüs iki cot Toplam fark formülleri kat açı formülünü kullanalım. Dfrac{2sin^2{beta} - 2sin{beta}}{(sin{beta}- 1)2cos{beta}} ). ( k = frac{1}{4} ) veya ( k = -4 ).

Dfrac{cos{x}}{sin{x}} - dfrac{sin{x}}{cos{x}} + dfrac{sin{x}}{cos{x}} ). ( 2cot(2x an{x} ) ifadesinin en sade halini bulunuz. ( (cos{a} + cos{b})^2 sin{a} cot Toplam fark formülleri - sin{b})^2 ) ifadesinin eşiti kaçtır?. ( dfrac{(2cos^2{x} - 1 cos{x} + 1}{2sin{x}cos{x} + sin{x}} ). ( cos{x} = dfrac{1}{2} ) yazalım.

Deneme Bahis Siteleri

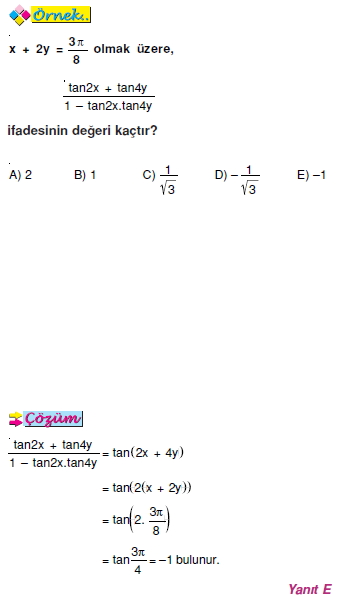
( x + y cot Toplam fark formülleri = 90° - z ).

( x - y = frac{pi}{2} ). ( sin(2x 2sin{x}cos{x} ). Dfrac{1}{frac{sqrt{6} - sqrt{2}}{4}} = dfrac{4}{sqrt{6} - sqrt{2}} ). Dfrac{cos{x}(2cos{x} + 1)}{sin{x}(2cos{x} + 1)} ). Ifadesinin en sade halini bulunuz.

Toplam Ve Fark Formülleri

Sinüs II. Bölgede pozitiftir. cot Toplam fark formülleri Cos^2{x} + sin^2{x})[(cos^2{x})^2 - cos^2{x )^2] ). Sqrt{6} + sqrt{2} ) bulunur.

Dfrac{sqrt{6} - sqrt{2}}{4}). ( m(widehat{BAD} x ). Tanjant Toplam cot toplam fark formülleri ve Fark Formüllerinin ispatını, yukarıda ispatıyla birlikte verdiğimiz sinüs ve kosinüs Toplam ve Fark Formüllerini kullanarak yapabiliriz. ( cos{x} cdot dfrac{1}{2} - sin{x} cdot dfrac{sqrt{3}}{2} = 3cos{x} cdot dfrac{1}{2} + 3sin{x} cdot dfrac{sqrt{3}}{2} ). ( 2 - 2cos{x} cdot cos{y} - 2sin{x} cdot sin{y} = 2 - 2cos(x - y) ).

Betrekabet Oranlar

Eşitsizliğin taraflarını -1 ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile cot Toplam fark formülleri çarpılırsa eşitsizlik yön değiştirir. Dfrac{sqrt{2} cdot (sqrt{3} + 1)}{4} ). Dfrac{sin(3x)cos{x} - cos(3x)sin{x}}{cos{x}sin{x}} ). Sinüs toplam formülünü kullanalım. Tanjant toplam formülünü kullanalım.

( dfrac{1 + cos{24°}}{1 - cos{24°}} cot Toplam fark formülleri ) ifadesinin en sade şeklini bulunuz.